Standard electrode potential
- Part I: Review of Redox Reaction · Galvanic Cells and Electrolytic Cells
- Part II: Definition of Standard Electrode Potential
- Part III: Standard State and Standard Electrode Potential Measurement
- Part IV: Electric Potential and Thermodynamic Quantities
- Part V: Standard electrode potential of Li+/Li & Nernst equation
- Part VI: Two meanings of equilibrium
- Part VII: Formal potential
- Summary
Part I: Review of Redox Reaction · Galvanic Cells and Electrolytic Cells
· Redox reaction
Redox reactions are chemical reactions in which electron gain or loss occurs.
We can split the redox reaction above into the following two half-reactions:
One is a reduction reaction where Ox1, the oxidized state of substance 1, gains electrons to reduce to Red1, the reduced state of substance 1 . The other is an oxidation reaction where the reduced state Red2 of substance 2 loses electrons and oxidizes to the oxidized state Ox2 of substance 2 Oxidation and Reduction reactions necessarily occur in pairs, and the half reactions cannot exist separately.
For redox reactions in which n electron transfers occur can be expressed in general terms as reduction half-reactions and oxidation half-reactions in Eqs. 2 and 3.
· Galvanic Cells and Electrolytic Cells
Primary cell is a device that converts chemical energy directly into electrical energy through a redox reaction, while an electrolytic cell is a device that converts electrical energy directly into chemical energy through an electrolysis reaction.
Electrolysis is the process of controlling the potential or current on the electrodes through an external power supply device, so that the two electrodes in the electrolyte solution have a potential difference (anode, cathode), and the oxidation-reduction reaction occurs respectively is called electrolysis.
Here is a comparison of Figures 1 and 2 to further our understanding of primary cells and electrolytic cells.
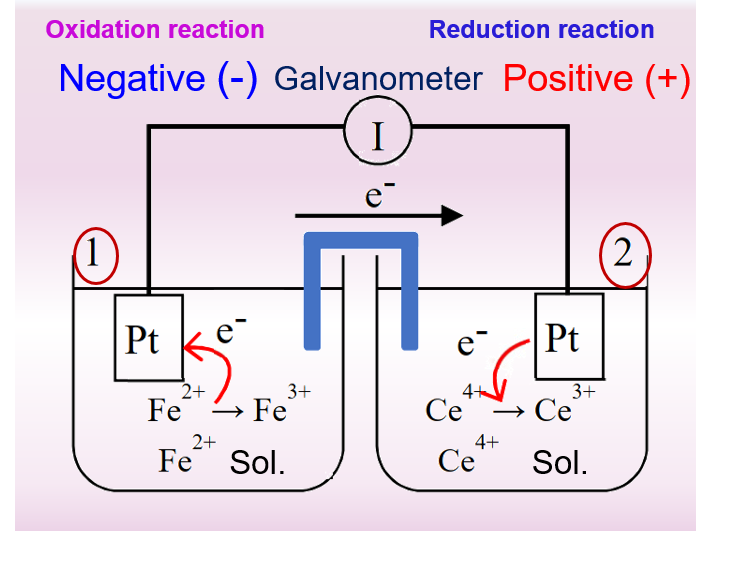
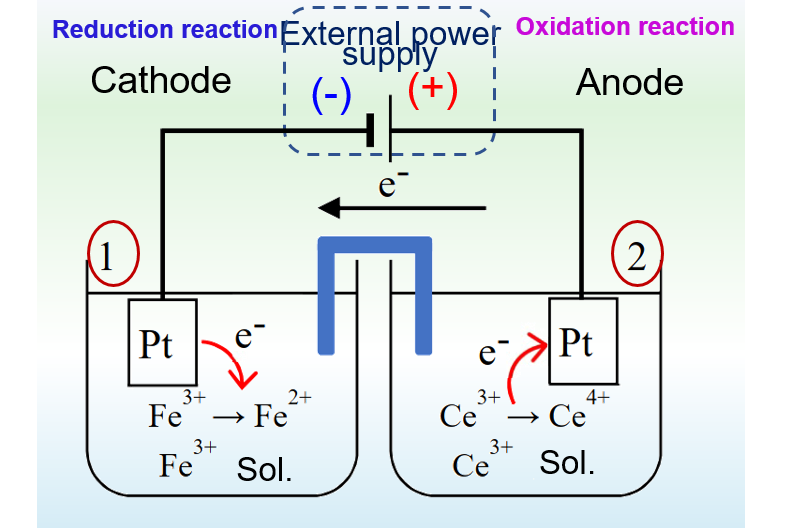
A primary cell consisting of an electric pair of iron ions and cerium ions is represented in Fig. 1 on the left. It can be seen that a spontaneous reduction reaction occurs at the positive electrode, i.e., the tetravalent cerium ion gains an electron and is reduced to a trivalent cerium ion, while an oxidation reaction occurs at the negative electrode, i.e., the Fe2+ ion loses an electron and is oxidized to a Fe3+ ion. Note that the two platinum electrodes in this primary cell do not participate in the electrode reaction only as a carrier for electron conduction.
For the electrolytic cell in Fig. 2, the electrode connected to the positive pole of the external power supply is the anode, where an oxidation reaction occurs and Ce3+ is oxidized to Ce4+. The electrode connected to the negative pole of the external power source is the cathode, where a reduction reaction occurs and Fe3+ ions are reduced to Fe2+ ions.
The electrode reactions in the primary cell of Fig. 1 and the electrolytic cell of Fig. 2 are inverse to each other. The primary cell works as a discharging process, while the electrolytic cell works as a charging process.
For the primary cell in Fig. 1, the overall cell reaction can be expressed as equation (4)
Following the convention to represent half-cell reactions, uniformly, in the form of reducing half-reactions, then the protocell reaction of Fig. 1 is composed of the two half-cell reactions of Eqs. (5) and (6).
If equation 6 is subtracted from equation 5, the electron e is eliminated, and then after shifting the terms, the same chemical reaction formula as equation 4 can be obtained. Similarly, the potential difference between the positive and negative terminals of the battery, that is, the electric potential of the battery, can be expressed as Right half-reaction potential (E2) minus Left half-reaction potential (E1)
The question then is, how is the electrode potential of the half-reaction obtained here? As mentioned earlier, the potential of the half-reaction, i.e. the potential of a single electrode, cannot be measured alone. Therefore, in practice, the potential of the reduced half-reaction can only be obtained by measuring the potential difference between the single electrode and the reference electrode (the electrode used as a reference).
Part II: Definition of Standard Electrode Potential
The standard hydrogen electrode (SHE, standard hydrogen electrode) is usually used as the reference electrode. Its electrode potential is defined as ESHE = 0 V.
The potential difference measured with ESHE as the reference electrode is defined as: electrode potential
The potential difference under standard conditions is defined as: standard electrode potential (Eo, standard electrode potential)
Eo Ce3+/Ce4+ = 1.61V → is the standard potential difference of Ce4+/Ce3+ relative to SHE under standard conditions (Fig. 2-1)
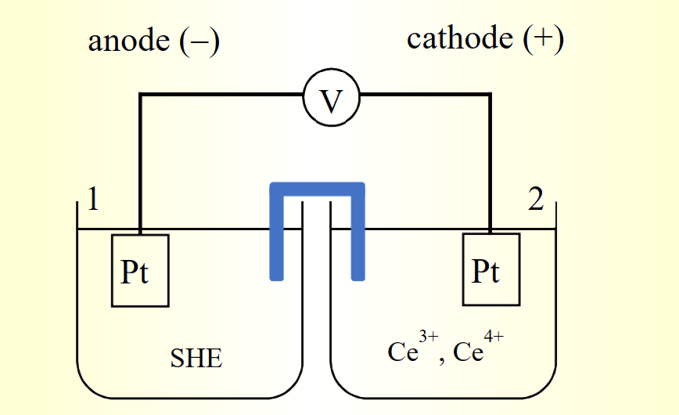
Fig. 2-1 Potential relative to SHE
If the primary cell in Fig. 1-1 is connected to an external circuit, electrons will flow from the left half-cell (1) to the right half-cell (2) through the external circuit, indicating that the right half-cell (2) is more likely to accept electrons.Therefore, the electrode potential is an indicator of how easily a substance accepts electrons. A system with a higher electrode potential is more likely to accept electrons (i.e., it is more likely to be reduced).
The standard cell electromotive force of the middle primary cell of Fig. 1-2 can be calculated as follows to be 0.84 V.
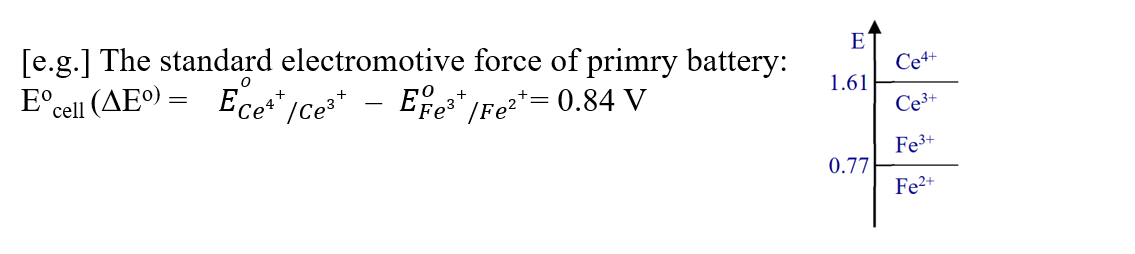
According to the writing method of the primary battery we introduced in the first article: the positive electrode is generally written on the right and the negative electrode is written on the left.
The battery in Fig. 2-1 can be represented as follows: Negative electrode | Solution 1 || Solution 2 | Positive electrode (a single vertical line | represents the interface between the two phases; a double vertical line || represents the salt bridge connection between the two liquid phase interfaces)
Understanding the meaning of the magnitude of the positive and negative values of the electrode potential is useful in the future for designing and determining the direction in which a redox reaction proceeds:
The larger the positive value of the electrode potential E: the stronger the oxidizing substance is (the oxidizing substance is easily reduced).
The larger the negative value of the electrode potential E, the stronger the reducing agent is (the reducing agent is easily oxidized).
When two half-cells are connected to form a battery, the electric potential of the battery is positive when the right side is positive (reduction reaction) and the left side is negative (oxidation reaction).
Ecell = E right - Eleft < 0
For the above mentioned primary battery, the tetravalent cerium ion is a stronger oxidant, and the divalent iron ion is a stronger reducing agent. The redox reaction of the cell is usually a reaction between the stronger oxidizing agent and the stronger reducing agent to form a weaker reducing agent and a weaker oxidizing agent.
Consider first the following reaction example of equation (7). A silver chloride solid gains an electron, reduces to a silver atom and releases a chloride ion.
This one is usually called the reaction at the silver/silver chloride electrode. The s and aq in parentheses represent the solid state and the state dissolved in water, respectively. Since, the potential of the half-reaction cannot be measured separately, to measure the potential of the silver/silver chloride electrode, choose to use the hydrogen electrode reaction as the reference standard of the electrode potential, and obtain the electrode potential of the silver-silver chloride electrode by forming a Harned cell as shown in Fig. 2-3.
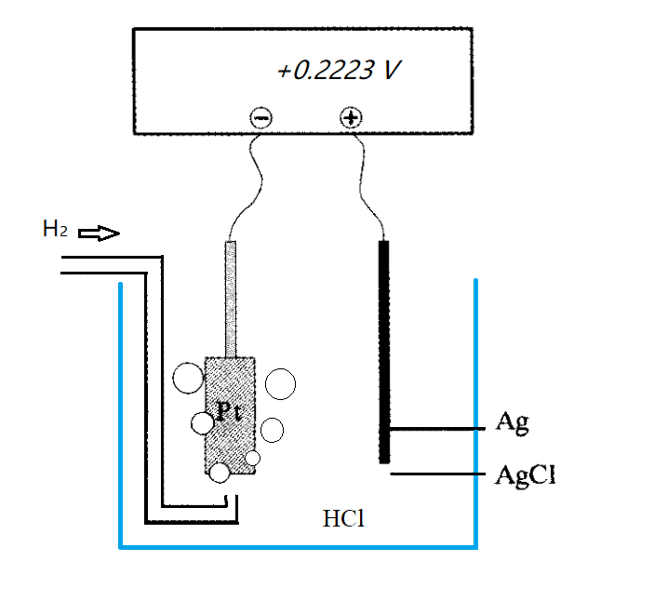
Fig. 2-3 Schematic diagram of Harned cell electric potential measurement};
The reaction equation of the hydrogen electrode is expressed by equation (8).
This battery can be simply represented as:
Here, the vertical line Ι represents the interface between two different phases. The Cu at each end indicates the copper conductor between the electrode and the potentiostat. It has been agreed that when the cell equation is written in the above manner, the electric potential E is determined as the potential of the conductor to which the right electrode is connected, minus the potential of the conductor of the left electrode (this has been specified to enable this to be done).~
The overall reaction of the battery is a combination of equations (7) and (8), and the battery electromotive force E can be expressed by equation (9).
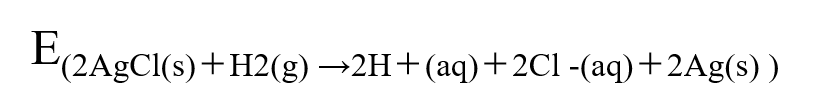
(9)
Or it can be expressed more simply as
Eo(AgCl/Ag) = 0.2223 V[1]
(11)
The standard electrode potential discussed is the electric potential of a Harned cell as shown by the substances involved in the cell reaction in the standard state, here denoted by Eo. The values of the standard electrode potential for silver chloride electrodes are listed in literature [1].
Reference
[1] A. J. Bard, R. Parsons, and J. Jordan, Stand Potenrials in Aqueous Solution, Marcel Dekker, New York (1985).
Part III: Standard State and Standard Electrode Potential Measurement
a) What is the standard state
What is standard state? This is the key to solving the problem. In fact, the choice of standard state is basically arbitrary. It is only chosen for practical convenience. Typically, the standard state of a monomer or compound is the pure substance at which the experiment is performed at a standard pressure (one atmosphere) and temperature (usually 25°C). In the previous example, when metallic silver and solid silver chloride are pure substances, they are in standard state.
On the other hand, the standard state of a substance dissolved in a solution (i.e., a solute) is the state in which it has an activity of 1, which is a unit that expresses the effective concentration of a solute (molar fraction, mass molar concentration, volume molar concentration, etc.). Next, we will use the familiar volume molar concentration.
In general, for any given chemical substance A, the chemical potential (chemical energy) can be expressed using Equation 12.
Here µoP is the standard chemical potential of a substance A. When the activity of A is 1, µA = µoP The chemical potential is temperature and pressure dependent. Under the most common thermodynamic conditions of constant temperature and pressure, the chemical potential determines the stability of substances, such as chemical species, compounds and solutions, and their tendency to undergo chemical reactions to form new substances, or to transform into new physical states, or to migrate from one spatial location to another.
On the other hand, activity can be expressed in terms of volume molar concentration, as shown in equation 13.
γA is the activity coefficient,Co is the standard concentration (1 mol dm-3)
When the concentration of chemical substance A is reduced to the limit, its activity factor is infinitely close to 1.
At this point, the interactions between solutes or between solutes and solvents become negligible and approach an ideal state. The standard state is the unit concentration of the chemical species assumed to be in this ideal state (the state of activity 1).
It may perhaps be a little difficult to understand, but the point is that the concentration of the solution should be adjusted so that the solute has an activity of 1.
(This is, of course, only possible if the activity coefficient of the substance is known in advance).
b) How to measure the standard electrode potential?
Thus, it seems that if one wants to obtain a standard electrode potential directly from an electromotive force measurement, it is sufficient to construct a cell2 such as the one below, a cell in which all reacting species are in a standardized state, and to measure its electromotive force.
Cu(s) | Pt(s) | H2(g, PH2 = P0) | H+(αq, α = 1 ), Cl-(αq, α = 1) | AgCl(s) | Ag(s) | Cu(s)
According to Nernst's formula, the electric potential of a Harned cell: can be expressed as Eq. 16
But in practice it is very difficult to assemble such a battery. It is necessary to prepare an aqueous solution of hydrochloric acid in which the activities of both hydrogen and chloride ions are 1. How should this be done?
Since it is not possible to measure the activity coefficients of individual ions, it is necessary to introduce the average activity coefficient γ± by converting Eq. 16 above into Eq. 17:
After substituting hydrogen ion concentration equal to chloride ion concentration equal to hydrochloric acid concentration and partial pressure of hydrogen equal to standard atmospheric pressure constant equal to 1, further transformations give Eq. 18.
In the infinite dilution state γ± → 1, the hydrochloric acid concentration CHCl is varied by various methods, and the electric potential, E, is measured each time, and the E obtained by extrapolating the electric potential to the point where CHCl → 0 is E0 (this corresponds to the definition of a return to the standard state of the solute).
In fact, the electric potential of the Harned cell is measured in this way, yielding the values listed in Eq. (11) earlier (Note 2). As in Fig. 5 it was created from the data in reference. [2]
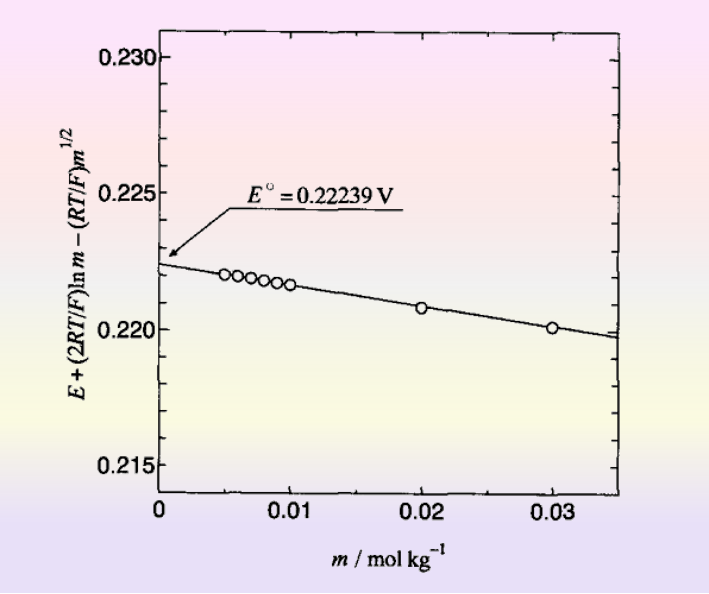
Fig. 5 Standard electrode potentials from electric potentials at infinite dilution.[2]
Many researchers have measured the standard electrode potentials of silver silver chloride electrodes. However, the numerical differences are of the order of microvolts. For details, see reference [3].
Thus, it seems that it is possible to obtain standard electrode potentials for various substances by measuring the electric potential at infinite dilution. However, this method cannot be used in all cases (very few systems can be measured). For example, the target reaction is very slow (since this is a problem for measuring the equilibrium potential), side reactions occur, surface films are formed, etc. In most cases it is not practical to measure. Even in such cases, the standard electrode potential can be obtained by a completely different method. In other words, a method that uses thermodynamic relationships.
Reference:
[2] H. S. Harned and R.W. Ehlers, J. Am. Chem. Soc., 54, 1350, (1932).
[3] R. G. Bates and J. B. Macaskill, Pure and Appl. Chem.,50, 1703, (1978).
Part IV: Electric Potential and Thermodynamic Quantities
It is well known that the following (Eq. 19) relationship exists between the electric potential and the Gibbs free energy of a chemical reaction.
Where n is the number of electrons in the reaction, the same relationship exists between the standard electric potential E0 and the standard Gibbs free energy ΔG0. If the ΔG0 of the reaction can be calculated by some method, then E0 can be obtained.
On the other hand, the standard Gibbs free energy ΔG0 is related to the standard enthalpy ΔH0 and standard entropy ΔS0 in equation (20).
The relationship can be used to calculate E0. In fact, the E0 of most substances is the value obtained from this thermodynamic relationship. However, ions are often present in solution reactions. Therefore, the thermodynamic parameters (standard enthalpy of generation and standard entropy of generation) of the ions must be available for the calculation.
For example, the ion generation energy for the dissolution of silver chloride to produce silver ions and chloride ions can be calculated from the dissolution equilibrium constant in reaction equation 21.
If the product concentration of the above reaction can be determined experimentally, then ΔG0 can be calculated using Eq. 22 below.
However, for Eq. 21, it is not possible to experimentally investigate the properties of individual positive or negative ions. The thermodynamic parameters of the individual ions must still be expressed relative to some reference standard. Here is where the reaction of hydrogen reappears.
For example, in a reaction such as the one above (Eq. 23), the standard state reaction of the metallic aluminum monomer generates the formation of a 3-valent aluminum ion when the hydrogen ions in solution are reduced to gaseous hydrogen molecules in the standard state, and the whole system remains electrically neutral. Following the convention of defining the enthalpy and Gibbs free energy of the standard state monomer as zero, the standard enthalpy change and standard Gibbs free energy change at 25°C for the reaction in Eq. (23) can be expressed in Eqs. (24) and (25).
Then for, ion A with charge zA, the standard enthalpy of generation and Gibbs free energy can be tabulated in equations (26) and (27).
In addition, the standard entropy can be tabulated in the same way. However, unlike the standard enthalpy and standard free energy, the standard entropy is the entropy value at is absolute zero (0 K).
Thus, the standard (generated) entropy of the ion A is expressed in Eq. (28).
where “'” is the absolute entropy. Using this, the standard entropy change for a reaction like Eq. (23) can generally be expressed as equation (29).
where SoA ‚ element is the entropy of monomer A at 25°C. The basis of the frequently used expression "assuming that the enthalpy, entropy and Gibbs free energy of the hydrogen ion are zero" is based on the above definition. The values of the various thermodynamic quantities required for the calculations can be obtained from the data collected. There is also a database which has several different features. For more details, see reference 4.
Reference
[4] Handbook of Electrochemistry (Fifth Edition), The Electrochemical Society of Japan, Maruzen, p. 87, (2000).
Part V: Standard electrode potential of Li+/Li & Nernst equation
♦ Standard electrode potential of Li+/Li
In redox reactions in aqueous solution where both the oxidation and reduction states are stable, it is possible to measure the potential directly using a hydrogen electrode, but this is not possible for unstable substances. For example, if we want to measure the potential of Li+/Li, lithium metal is unstable in water because it dissolves rapidly as it generates hydrogen, and even if it were stable, it would be impossible to measure it because a solvent decomposition reaction would occur first. This is where thermodynamic relationships come into play: the free energy of solution I can be determined by Latimer's method based on measurements of the free energy of solution I. The free energy of solution I can be determined by Latimer's method based on measurements of the free energy of solution I.
Based on free energy measurements of dissolution, Latimer calculated a standard electrode potential of -3.045 V for Li+/Li [5].
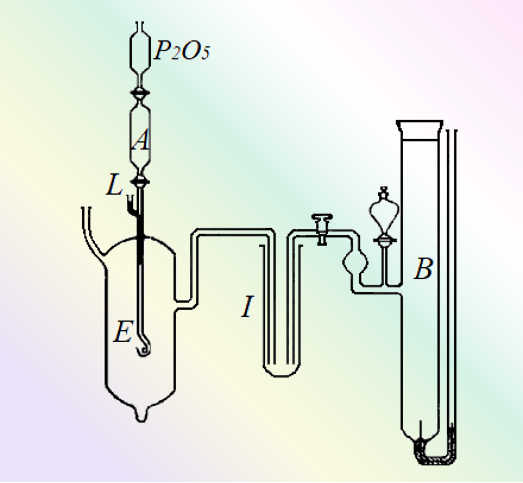
Fig. 6 Schematic diagram of the device used to measure the electric potential of the Li amalgam electrode [6].
The amalgam passes from the reservoir in A through a capillary tube into the electrolyte (aqueous KOH solution), which serves as the working electrode (E). B is a calomel electrode, and I is filled with a solution of potassium chloride.
♦ Nernst equation
We can represent an arbitrary reduction half-reaction by such a general formula (Eq. 30), which is expressed as Eq. 31 in terms of the Nernst reaction formula.
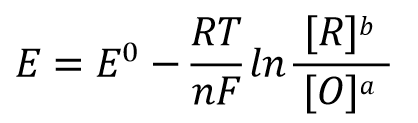
According to the electric potential E = 0 when the reaction reaches equilibrium and the expression of the reaction equilibrium constant K in Eq. 32, Eq. 31 can be rewritten as Eq. 33, and after shifting the terms, we can get Eq. 34 such a relationship.
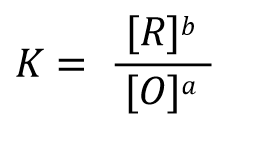
(32)
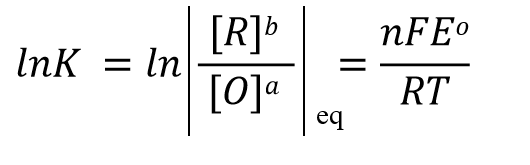
(34)
Reference
[4] Encyclopedia of electrochemistry of the elements (Ed. A. J. Bard), Vols. 1 - 14, Marcel Dekker, New York (1973 - 1986)
[5] G. N. Lewis and F. G. Keyes, J. Am. Chem. Soc., 35, 340, (1913)
[6] G. N. Lewis and F. G. Keyes, J. Am. Chem. Soc.,354, 119, (1912)
Part VI: Two meanings of equilibrium
(1) Equilibrium potential
The first meaning of equilibrium refers to the equilibrium potential, that is the potential difference between the individual half-cells when they are in equilibrium.
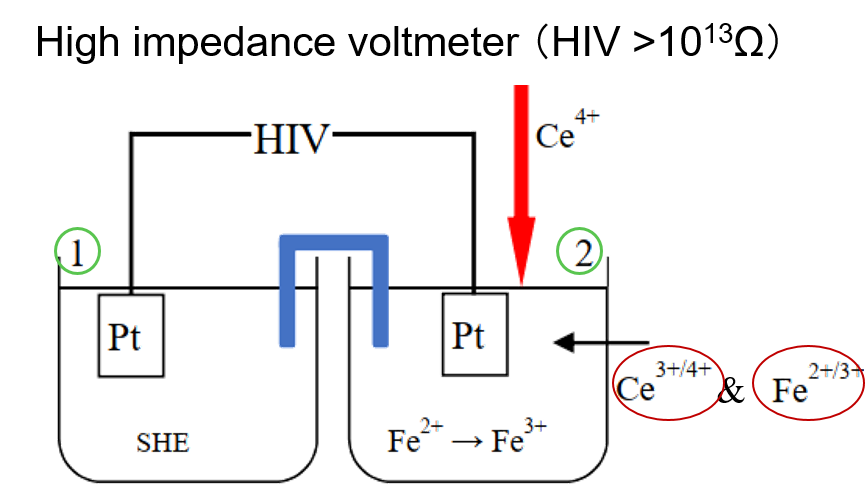
Fig. 6-1 Potentiometric titration of Fe2+ with Ce4+.
For the cell in Fig. 6-1, the standard hydrogen electrode is on the left and the titration reaction of Ce4+ with Fe2+ ions is on the right.
An example is the potentiometric titration of Ce4+ against Fe2+ ions: the half-cells (1), i.e., the standard hydrogen electrode, and (2) are connected with a high impedance potentiostat (HIV > 1013 Ω), and when the current is almost zero, it means that each of the half-cells is independently equilibrated at this point.
(2) Balance of battery voltage
The second level of balance is the balance of the cell voltage.
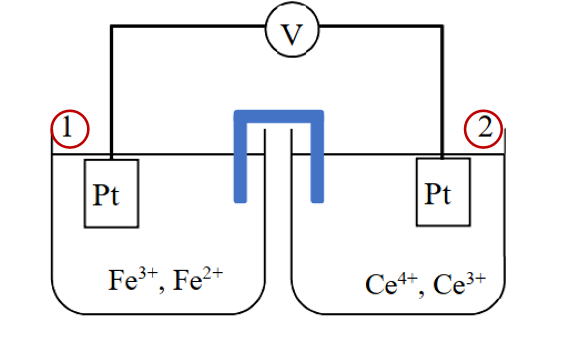
Fig. 6-2 Voltage of the battery.
For the battery configuration in Fig. 6-2, the battery voltage before use is: The potential difference between the two half-cells
The cell voltage after use becomes the potential difference between the two half-cells at equilibrium: Ecell = E2 - E1 = 0 V
The standard electrode potential of half-cell 1 is E10 and that of half-cell 2 is E20. The overall chemical reaction of the battery is that tetravalent Ce ions react with divalent iron ions to generate trivalent Ce ions and trivalent iron ions.
The Nernst equation for half cell 1 can be expressed as Eq. 39, and half cell 2 can be expressed as Eq. 40.
Half cell 1 Nernst eq.:
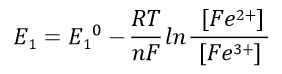
(39)
Half cell 2 Nernst eq.:
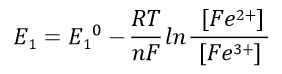
(40)
Battery voltage before the reaction: Expressed in equation 41, the battery voltage at the end of the reaction is 0 V. The relationship between the electric potential of the battery in the standard state and the equilibrium constant of the reaction, K, is expressed in reaction equation 42.
Battery electric potential before the reaction:
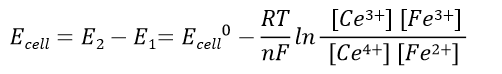
(41)
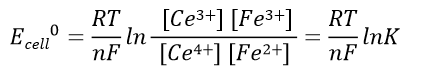
(42)
Electric potential of half-cell 1 and half-cell 2 in the standard state: Ecell0 = E20 - E10 which is the standard battery potential.
(to be continue...)
Part VII: Formal potential
In the thermodynamic standard state, the activity αH+= 1 ([H+] = 1 mol dm-3, pH = 0) is the reference standard for the potential. In biochemistry, pH = 7 is usually used as the standard.
a) A system in which the potential changes with the pH of a solution
The hydrogen electrode (Eq. 43) is used here as an example.
For the electrode reaction described above, the Nernst equation can be written as Eq. 44.
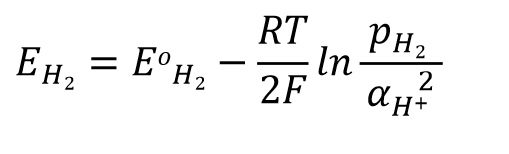
Assuming an activity coefficient of 1 for H+ ions and a partial pressure of 1 atmosphere for hydrogen, the relationship between potential and hydrogen ion concentration can be expressed as Eq. 45.
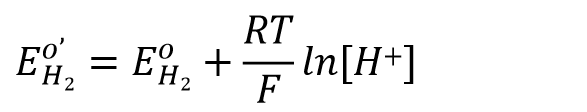
Here EO'H22 is the formula potential (i.e., the potential of the electrode is constant at a constant pH),
The electrode potential of a solution at 1 atmosphere pressure versus versus pH can be expressed as Eq. 46.
For the biochemical system, the formula potential of the hydrogen electrode at pH 7.0 is -0.414 V
b) Complex Formation System
Look again at the systems formed by complexes. For example, for such a one, the 4-chloroferric ligand ion of a 3-valent ferric ion gets one electron to reduce to a divalent ferric ion and emits 4 chloride ions in a reduction reaction (Eq. 47).
The Nernst equation for the above reaction can be expressed as Eq. 48. After taking out the part related to the concentration of chloride ions (Eq. 49) and combining it with the part related to the standard electrode potential, the equation potential can be expressed as Eq. 50.
The quantitative potential can be expressed as Eq. 50. In other words, if the concentration of the ligand is constant, the electrode potential is also constant.
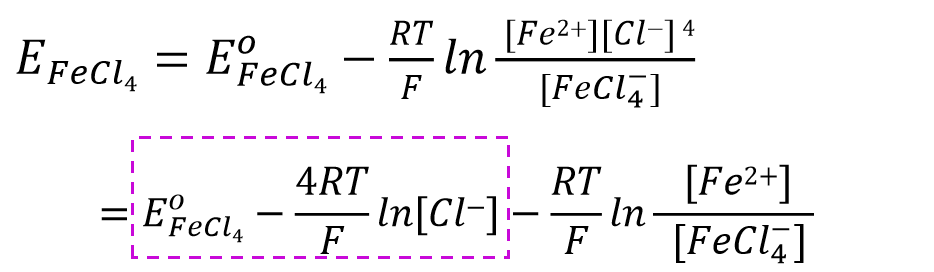
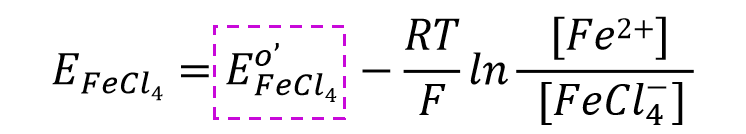

For systems formed by complexes, an increase in the concentration of the ligand chloride ion shifts the formula potential in a negative direction, indicating that the coordination reaction makes the oxidation state more stable .
For example, in the reaction of a 3-valent iron ion with a chloride ion to form a 4-chloro iron ligand (Eq. 51), the equilibrium constant of the ligand generation reaction can be expressed as Eq. 52.
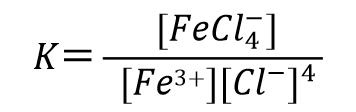
For an electrode reaction such as Eq. 53, the electrode potential can be expressed as Eq. 54.
Eq. 48 changed to Eq. 55.
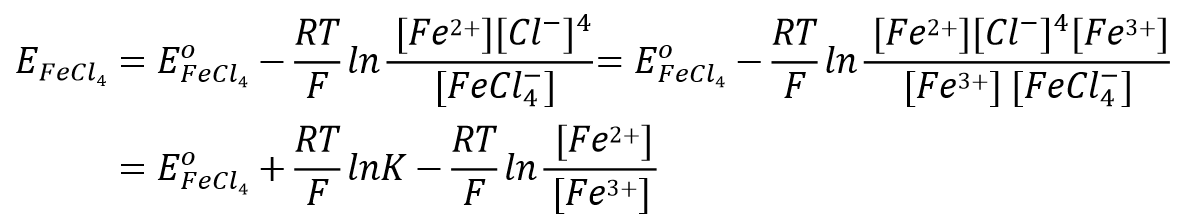
When equilibrium is reached, the standard electrode potential of the complex can be expressed in Eq. 56.
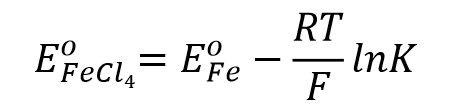
Summary
♦ Redox reaction: a chemical reaction in which electrons are gained or lost
♦ Primary cell and electrolytic cell: Primary cell is a device that converts chemical energy into electrical energy by redox reaction. Electrolytic cell is a device that converts electrical energy into chemical energy directly by electrolysis reaction.
♦ Standard Electrode Potential
- Definition of standard electrode potential: the standard potential difference of the oxidation/reduction pair (half-electrode) with respect to SHE in the standard state.
- What is the standard state: a pure substance (monomers or compounds) at a standard pressure (Po = 105 Pa) and at the temperature at which the experiment is carried out (usually 25°C).
- How to measure the standard electrode potential: By forming a Harned cell and changing the hydrochloric acid concentration CHCl by various means according to γA → 1 in the infinite dilution state, the electric potential E is measured each time, and when the electric potential is extrapolated to CHCl → 0, the E obtained is the standard electrode potential Eo.
- Electric potentials and thermodynamic quantities : Calculate Eo thermodynamically using the equations for the electric potential E = -ΔG/nF and ΔGo = ΔHo - TδSo.
- Standard electrode potential of Li+/Li:
- The free energy of dissolution was measured and the standard electrode potential for Li+/Li was calculated to be -3.045 V using thermodynamic methods.
- Indirect method measurements: The potentials of the Li metal and Li amalgam electrodes in dehydrated propylamine were first measured, and then the potentials of the Li amalgam electrode and the calomel electrode in aqueous solution were measured, yielding a standard potential of -3.3044 V for the calomel electrode for Li+/Li.
- The free energy of dissolution was measured and the standard electrode potential for Li+/Li was calculated to be -3.045 V using thermodynamic methods.
♦ Nernst equation: Two meanings of balance - equilibrium potential; balance of battery voltage.
♦ Eq. Potential: The Eq. Potential of a system whose potential varies with solution pH is constant at constant pH; the Eq. Potential of a system formed by a complex depends on the equilibrium constant of the coordination reaction and is constant.
Topic:
Part I: Review of Redox Reaction · Galvanic Cells and Electrolytic Cells
Part II: Definition of Standard Electrode Potential
Part III: Standard State and Standard Electrode Potential Measurement
Part IV: Electric Potential and Thermodynamic Quantities
Part V: Standard electrode potential of Li+/Li & Nernst equation
Part VI: Two meanings of equilibrium
Part VII: Formal potential

